头条
「因子」即技术分析中的「指标」、人工智能机器学习的「特征」,是决定加密货币收益率涨跌的原因。
撰文:LUCIDA & FALCON
在去年 6 月份,我设想了用多因子模型去择币的简单构思。
一年后,我们已经着手研发针对加密资产市场的多因子策略,并把整体的策略框架写成系列的文章《用多因子策略构建强大的加密资产投资组合》。
「因子」即技术分析中的「指标」、人工智能机器学习的「特征」,是决定加密货币收益率涨跌的原因。
我们团队把加密货币领域常见的因子类型:基本面因子、链上因子、量价因子、衍生品因子、另类因子和宏观因子。
挖掘和计算「因子」的最终目的是为了准确计算资产的预期收益率。
起源:单因子模型——CAPM
因子研究可追溯于 20C60S,资本资产定价模型(Capital Asset Pricing Model, CAPM)问世,该模型量化了风险如何影响一个公司的资本成本从而影响预期收益率。根据 CAPM 理论,单个资产的预期超额收益可由以下的一元线性模型决定:
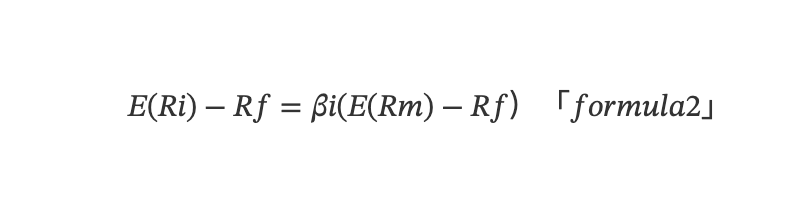
E(Ri)是数学期望, Ri 为资产的收益率,Rf 为无风险收益率, Rm 为市场组合的收益率,βi = Cov(Ri,Rm)/Var(Rm) 体现资产收益对市场收益的敏感程度,也称资产对市场风险的暴露程度。
补充理解:
金融市场中,所谈及的「风险」和「收益」本质是同类东西。
从统计学角度,更详细的理解 βi
CAPM 可看成是无截距项的双变量回归模型 Yi = β1 + β2 · X (β1 = 0),利用普通最小二乘估计法(OLS)求出模型参数的估计值,其中β1 = β2 = Σ(X-μX)(Y-μY)/ Σ(X-μX)² = Cov(X,Y)/Var(X) 。
β1 衡量解释变量(市场收益率)变动以单位,被解释变量(资产 i 的收益率)平均变动的程度,金融领域将该变动程度解释为 Y 对 X 的「敏感」或「暴露」程度。
β>1 放大市场波动
β = 1 与市场波动完全相同
0<β<1 与市场同向波动,但比市场波动小
β≤ 0 与市场反向波动
1.从金融学风险和收益的角度,更详细的理解βi
投资组合有两类风险,系统性风险(即市场风险、不可抵消风险)和非系统性风险(可抵消风险)。 βi 是系统性风险,无论如何构造资产组合,该风险是该系统特有的,无法抵消。下文提及的 αi 则是非系统性风险,可通过构造不同的策略来对冲掉。
CAPM 模型是最简单的线性因子模型,指出资产的超额收益只由市场 组合(市场因子)的预期超额收益和资产对市场风险的暴露大小决定。该模型为后续大量线性多因子定价模型的研究奠定基理论础。
发展:多因子模型——APT
在 CAPM 基础,人们发现不同资产的收益率受多个因子影响,套利定价理论(Arbitrage Pricing Theory, APT)问世,构建线性多因子模型:
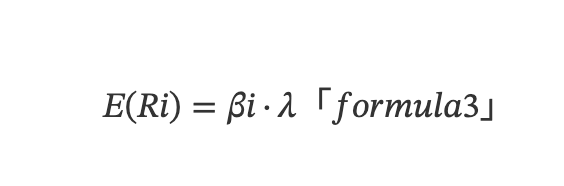
其中,E(Ri) 表示资产 i 的预期收益,λ表示因子预期收益(即因子溢价)。公式 (2) 利用 E(Ri) 代替 CAPM 模型中的 E(Ri) - Rf 来表示预期收益,利用多空对冲构建的资金中性投资组合资产,Rf 被抵消,整个资产的预期收益率就是多头和空头预期收益率之差,因此用 E(Ri) 表示更具一般性。
成熟:多因子模型——Alpha 收益 & Beta 收益
综合考虑金融市场实际存在的定价误差和 APT 模型,从时序角度上看,单个资产的预期收益率由以下的多元线性模型决定:
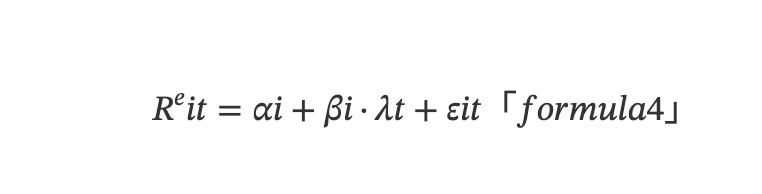
其中,Rᵉit 表示 t 时刻资产 i 的收益,λt 表示 t 时刻因子收益率(即因子溢价),εit 表示 t 时刻的随机扰动。αi 表示资产 i 的实际预期收益率和多因子模型隐含的预期收益率之间的定价误差,若统计上显著偏离零,则代表了获得超额收益的机会。βi = Cov(Ri,λ)/Var(λ) 表示资产 i 的因子暴露或因子载荷,刻画了资产收益对因子收益的敏感程度。
多因子模型关注资产预期收益率在截面上的差异,本质是关于均值的模型,而预期收益率是收益率在时间序列上的平均。基于 (3) ,可推导出截面角度的多元线性模型:
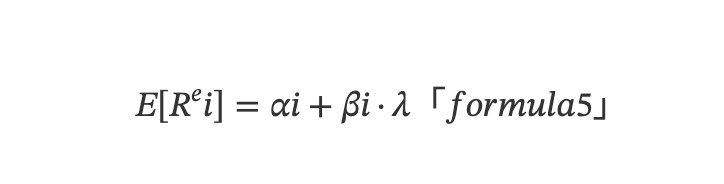
其中,E[Rᵉi] 表示资产 i 的预期超额收益,εit 在时序上取平均,则 E(εit)=0。
补充理解:
从学术界角度出发,根据市场有效性理论,一个有效的资产组合应该是可抵消风险完全为 0,实际收益率等于预期收益率,且预期资产收益率只取决于市场的系统性风险,即 E[Rᵉi] = βi · λ,不存在超额收益率(Abnormal Return, AR),即 AR = Ri - E(Rᵉi) = 0。但现实的金融世界通常是市场非有效的,存在超额收益率,即 AR = α。
假设投资组合由 N 资产构成,并将每个资产 i 应的因子收益λ 按照不同因子展开,得到以下多因子模型的组合收益率:
Rp = ∑ᴺᵢ₌₁Wi(αi+∑ᴹⱼ₌₁βᵢⱼfᵢⱼ)
其中,Rp 为组合的超额收益,Wi 是每份资产占组合的权重,βij 是每份资产在每个因子上的风险暴露,λ = ∑ᴹⱼ₌₁βᵢⱼfᵢⱼ),fᵢⱼ 是每份资产的每个因子每单位因子载荷对应的因子收益率。
结合统计学知识,该模型隐含三层假设:
每个资产的 Beta 收益和 Alpha 收益不相关:Cov(αi,βiλ)=0
不同资产间的特质收益率也不相关:Cov(αi,αj)=0
因子一定和资产收益率有关:Cov(Rᵉi,βiλ)≠0
对于 Beta 收益和 Alpha 收益的综合解释:
结合具体的金融市场,βiλ 是归属于大盘整体表现的 Beta 收益,αi 则是由资产自身特定带来的 Alpha 收益,即跑赢大盘多少个点。而每个资产的收益率则是由 Beta 收益和 Alpha 收益组成,人们可利用多因子模型中每个资产对应的αi 值来对每个资产打分或赋予权重,从而构造投资组合,并利用期货对 Beta 收益部分做空来对冲风险,从而获得 Alpha 收益。
构造投资组合时需在组合的风险和收益间取平衡,需要将以上模型转化为带约束的规划问题来求解。组合的风险即组合的波动率 σ²p,以下对σ²p 进行推导。涉及组合构建的详细分析则在「风险组合优化」部分阐述。
基于公式 (3) 的矩阵表达式 Rp = W(β ∧ + α),可得到组合的波动率:
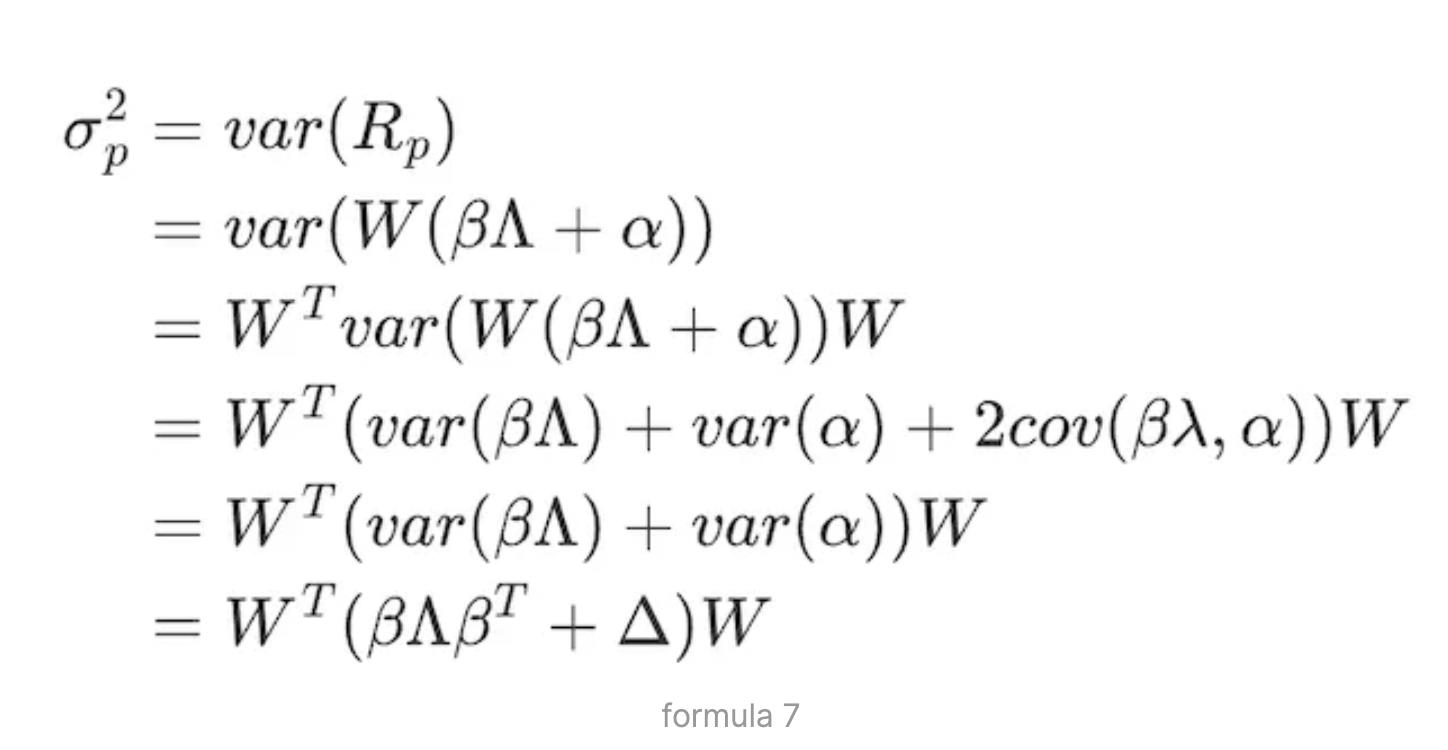
其中,W 是资产的权重矩阵,β是因子的权重矩阵,表示 N 个资产在 K 个风险因子上的因子载荷矩阵 N×K:

∧ 表示 K 个因子的因子收益率协方差矩阵 K×K :

由假设 3,不同资产间的特质收益率也不相关,可得Δ 矩阵为:
